Copyright © 2006-2022 高顿教育, All Rights Reserved. 网站地图
考研数学真题这个=1代表的是什么等于1啊?
老师,可以帮我看下例13吗,这个=1代表的是什么等于1啊?

 A同学
A同学- 2021-03-23 21:43:42
- 阅读量 368
-
老师 高顿财经研究院老师高顿为您提供一对一解答服务,关于考研数学真题这个=1代表的是什么等于1啊?我的回答如下:
你好同学,
这里的1是假设的工程量为1。
验证过程可参考:
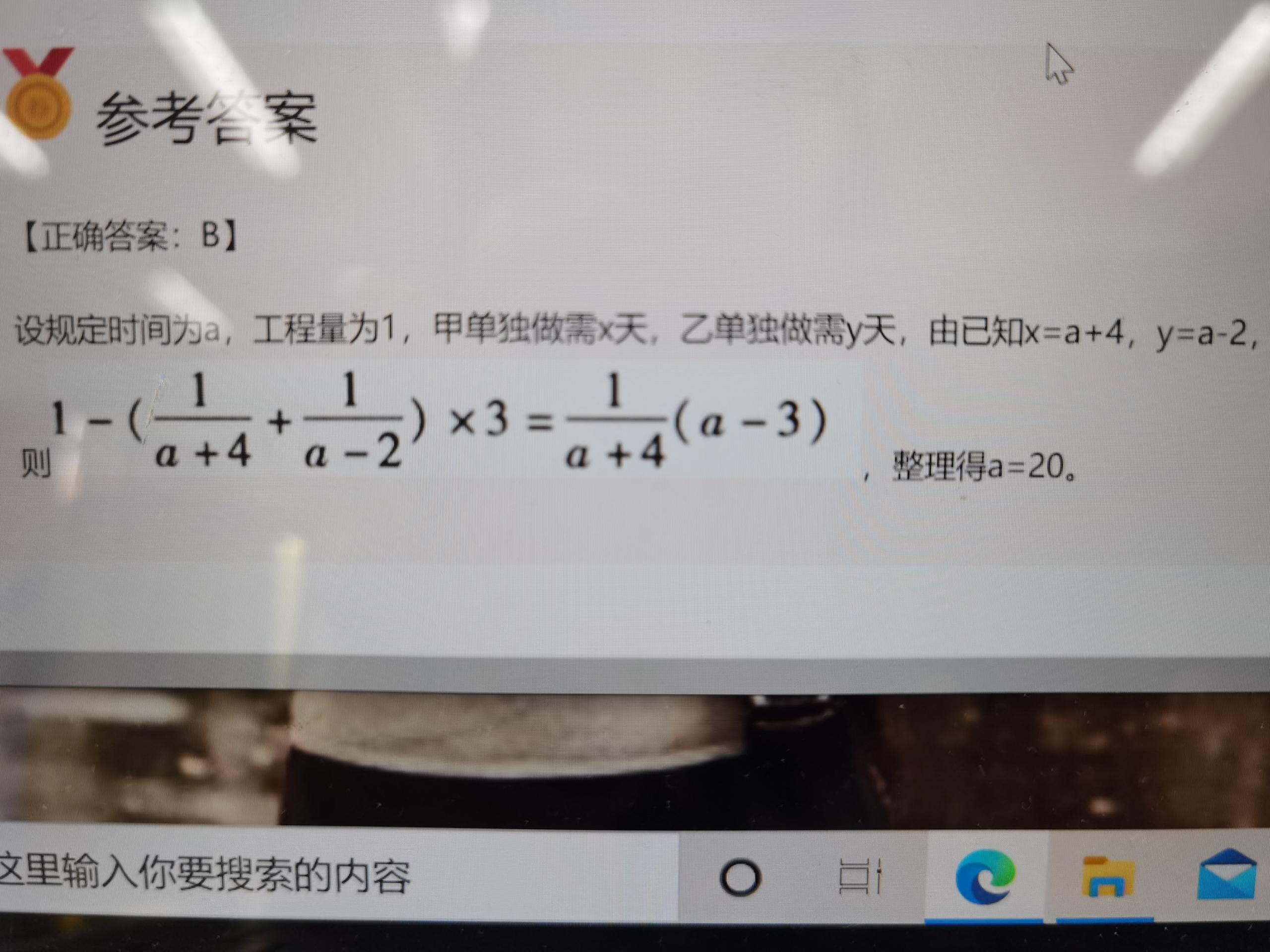
以上是关于考研,考研数学真题相关问题的解答,希望对你有所帮助,如有其它疑问想快速被解答可在线咨询或添加老师微信。2021-03-24 10:35:55
-
考研数学真题:这一步是洛必达推导出来的吗?
这一步是如何推导出来的?...
-
考研数学真题:洛必达详细变换过程吗?
这一步看不懂,麻烦老师写一下详细变换过程...
-
考研数学真题:这种分子为1的怎么拆项,有没有公式啊?
这种分子为1的怎么拆项,有没有公式...
-
考研数学真题:为什么用泰勒和用洛必达得到的结果不一样啊?
老师,您好,请问划线的那个式子为什么用泰勒和用洛必达得到的结...
-
考研数学真题: 课题一函数的第4题怎么理解啊?
习题集上 课题一函数的第4题不是很懂...
-
考研数学真题:函数里的第二道题里的x<=0吗?
老师我想请问一下高等数学习题集里的1.函数里的第二道题里的答...
-
考研数学真题:为什么比x的二次方高的项都不用求了吗?
为什么比x的二次方高的项都不用求了?比x的二次方高的项是都并...
-
考研数学真题:后半部分In的求导是怎么一步得出来啊?
老师您好。后半部分In的求导是怎么一步得出来?复合函数求导我...
-
考研数学真题:这步是用的什么数学公式呀?
想问一下这步是用的什么公式呀...
-
考研数学真题:怎么推导这个数学式子啊?
不会推导这个式子...
-

2023扬州大学教育学原理考研研究方向有几个?共6个
2023扬州大学教育学原理考研研究方向有6个,对扬州大学教育学原理考研感兴趣的同学们,如果对相关信息还不清楚,快来看看高顿小编整理的2023扬州大学教育学原理考研研究方向的有关内容吧!希望对大家有所帮助。
2022-12-07 09:36:15 -

西南石油大学925计算机学科综合2023考研自命题考试大纲及参考书目
西南石油大学925计算机学科综合2023考研自命题考试大纲及参考书目已经发布,考试大纲包含了考试范围、考试要求、考试形式、试卷结构等重要信息,对考生具有重大的参考意义。
2022-12-07 09:32:56 -

2023扬州大学兽医学院(比较医学研究院)考研拟招人数是多少?
2023扬州大学兽医学院(比较医学研究院)考研拟招人数是105人。根据其考研招生专业目录可知,扬州大学兽医学院(比较医学研究院)学硕专业有基础兽医学、预防兽医学、临床兽医学、兽医生物信息学、兽医公共卫生学、实验动物学与比较医学,专硕专业有兽医硕士。下面是高顿小编整理的2023扬州大学兽医学院(比较医学研究院)考研拟招人数的相关内容,一起来看看吧!
2022-12-07 09:17:29 -

2023年北京航空航天大学计算机考研招生简章!点击查看
2023年北京航空航天大学计算机考研招生简章可以参照2023年北京航空航天大学硕士研究生招生简章,考研招生简章包含了院校简介、报考条件、报名时间、学费、学制、奖助体系等详细信息。
2022-12-07 09:04:01 -

2023年东华理工大学计算机考研招生简章!点击查看
2023年东华理工大学计算机考研招生简章可以参照2023年东华理工大学硕士研究生招生简章,考研招生简章包含了院校简介、报考条件、报名时间、学费、学制、奖助体系等详细信息。
2022-12-07 08:59:52
-
考研数学AB=0怎么证明r(A)+r(B)小于等于n?
教师回复: 可以按照这个来理解因为AB=0,所以矩阵B的列向量都是线性方程组AX=0的解;则矩阵B的列向量组的秩,不大于方程组AX=0的基础解系的个数,也就是说矩阵B的列向量组可以由AX=0 的基础解系线性表示,所以R(B) <= n-R(A),故R(A)+R(B)小于等于n。
-
考研数学题中为什么正向级数收敛其奇偶项也收敛呢?
教师回复: 是这么理解的:正项级数收敛就意味着它们加起来是等于一个常数的,而偶(奇)数项只是正项级数的一部分,那么它们加起来肯定也是一个常数,所以是收敛的。严格的证明需要按照正项级数收敛的定义,用单调有界定理来证明。
-
考研数学真题ln(1-x)的泰勒展开式是什么呀?
教师回复: 这里应该套用的是ln1+x的公式,因为x趋于0的,然后可以把-x带入
-
考研英语句子“What a difference a day makes!”能否译为“一天的变化真大
教师回复: 这是个感叹句,使用了倒装,顺过来说是 a day makes a difference. 某一天产生了重要的作用/ 某一天发生了一个变化。 用感叹语气,则是 某一天产生了多么大变化啊!(某一天和平时非常不一样);翻译则调整表达为: 多么与众不同的一天啊! 多么特别的一天啊!
-
为什么x趋于0时,为什么ln(cosx)等于-1/2 x^2?
教师回复: x趋于0,cosx的极限是1,所以ln(cosx)=ln(1-1+cosx),等价无穷小为-1+cosx,也就是等价无穷小为-1/2 x^2
- 金融类
- ACCA
- 证券从业
- 银行从业
- 期货从业
- 税务师
- 资产评估师
- 基金从业
- 国内证书
- CPA
- 会计从业
- 初级会计职称
- 中级会计职称
- 中级经济师
- 初级经济师
- 其它
- 考研




