Copyright © 2006-2022 高顿教育, All Rights Reserved. 网站地图
考研数学:不太明白解析中标注部分?
不太明白解析中标注部分,为什么先用换元,后面又可以直接换回来了但是积分下限又不变?
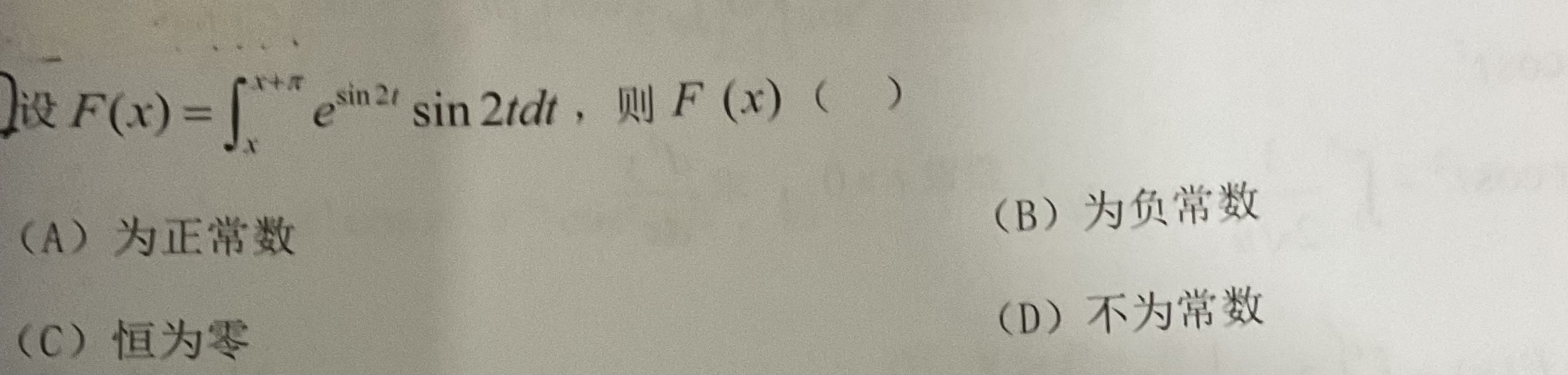
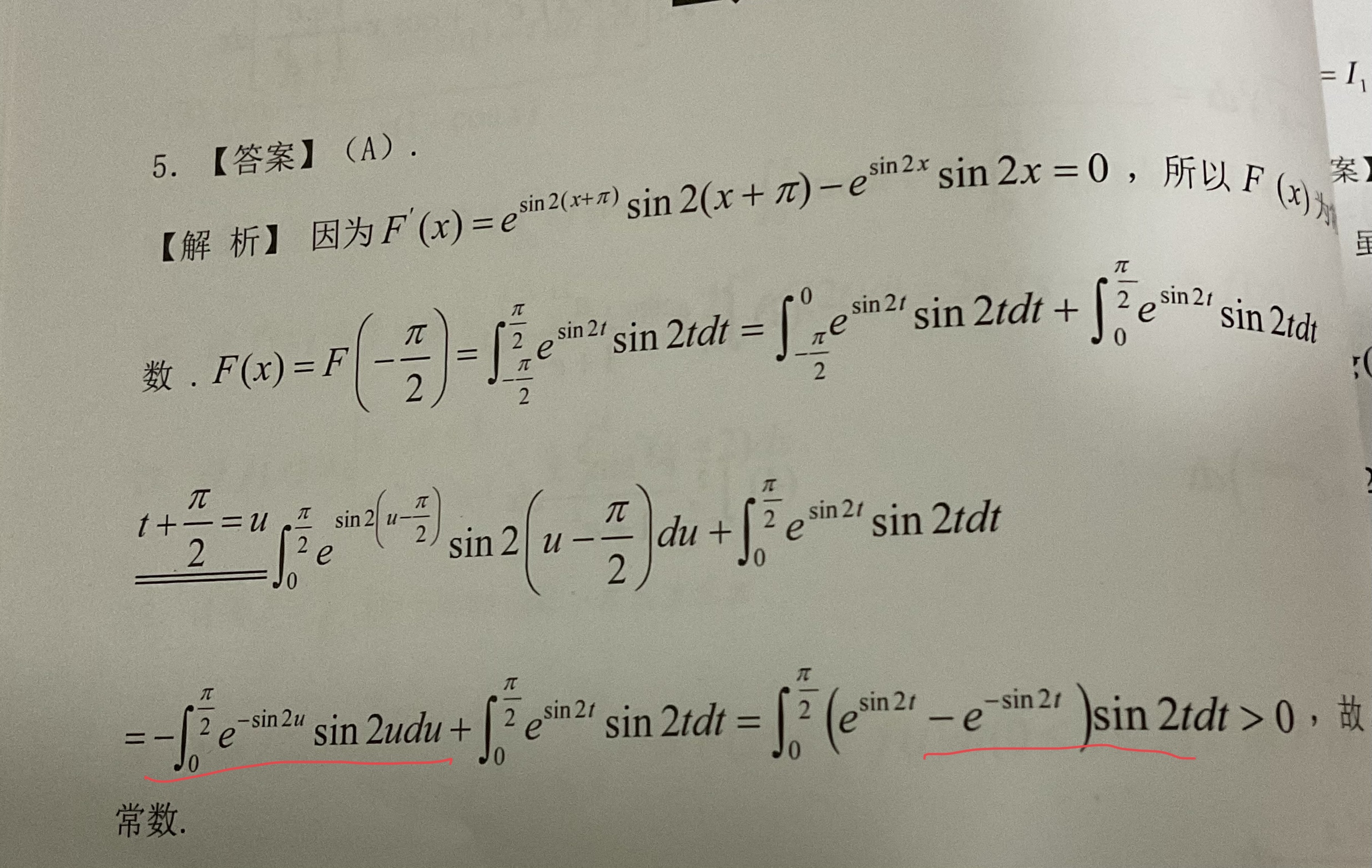
 凌同学
凌同学- 2021-02-09 20:36:36
- 阅读量 330
-
老师 高顿财经研究院老师高顿为您提供一对一解答服务,关于考研数学:不太明白解析中标注部分?我的回答如下:
[quote][/quote]
以上是关于考研,考研数学相关问题的解答,希望对你有所帮助,如有其它疑问想快速被解答可在线咨询或添加老师微信。2021-02-09 22:34:35 -
收起
 凌同学学员追问好的谢谢老师2021-02-10 08:25:37
凌同学学员追问好的谢谢老师2021-02-10 08:25:37
-
考研数学题:这里为什么x0不是x<1?
为什么x0,不是x<1...
-
考研数学题:为什么先取对数再求导是错的?
为什么先取对数再求导算出来的结果是错的?...
-
考研数学:取对数求导算出来的结果与先化指数的区别是?
为什么改题用取对数求导算出来的结果和化为指数函数形式再求导得...
-
考研数学:为什么分子趋向于0时分母也趋向于0?
老师 为什么 分子趋向于0时 分母也趋向于0呢...
-
考研数学:tanx的定义域怎么变成tan(x+1)的定义域?
第一题的第二题和第五题,第二题,tanx的定义域怎么变成ta...
-
考研数学题:无穷小量-有界量=极限不存在吗?
老师您好,我的问题是:考研数学讲义高等数学基础第73页例4....
-
考研数学:遇到好多三角函数时化成什么样子合适?
题目答案如图一图二(有tanx)。我的答案如图三(没写tan...
-
考研数学:为什么y求二阶导就可以得出分段函数?
老师,为什么y求二阶导后就可以得出是分段函数? 不是很懂...
-
考研数学:展开时为什么cosx是从0开始而ln(1+x)从1?
展开时为什么cosx是从0开始而ln(1+x)从1开始呢...
-
考研数学题:sinx方不可以等价替换吗?
老师,看我红笔写的,有问题吗,我咋感觉没有问题,但是答案对不...
-

2023重庆三峡学院903土木工程材料考研大纲一览!
重庆三峡学院903土木工程材料2023考研大纲已经发布,为了帮助大家能够及时地掌握其中的关键信息,高顿小编整理了2023重庆三峡学院903土木工程材料考研大纲的有关内容,一起来看。
2022-12-26 11:22:01 -

2022贵州中医药大学考研复试笔试科目发布!
2022贵州中医药大学考研复试笔试科目已发布!为了给23考研党作为参考,小编整理了2022贵州中医药大学考研复试笔试科目的有关内容,具体如下:
2022-12-26 11:11:01 -

2022贵州中医药大学考研调剂基本要求已出!
2022贵州中医药大学硕士研究生招生考试调剂公告已出!高顿小编整理了其调剂基本要求、各专业接收调剂考生专业要求、调剂方式的内容,感兴趣的同学们快来看看吧!
2022-12-26 10:57:20 -

2023贵州中医药大学考研初试科目有哪些?
2023贵州中医药大学考研初试科目有哪些?掌握这一信息对于报考贵州中医药大学硕士研究生的同学有很大的参考意义,所以小编整理了2023贵州中医药大学考研初试科目的有关内容,希望对大家能有所帮助。
2022-12-26 10:29:34 -

详解!2023年在职考研MBA报考流程一览
详解!2023年在职考研MBA报考流程一览!在职考研MBA分为国内考研和国际考研,相对应的报考流程有所区别。下面是具体内容。
2022-12-26 10:28:54
-
考研数学题中为什么正向级数收敛其奇偶项也收敛呢?
教师回复: 是这么理解的:正项级数收敛就意味着它们加起来是等于一个常数的,而偶(奇)数项只是正项级数的一部分,那么它们加起来肯定也是一个常数,所以是收敛的。严格的证明需要按照正项级数收敛的定义,用单调有界定理来证明。
-
考研数学AB=0怎么证明r(A)+r(B)小于等于n?
教师回复: 可以按照这个来理解因为AB=0,所以矩阵B的列向量都是线性方程组AX=0的解;则矩阵B的列向量组的秩,不大于方程组AX=0的基础解系的个数,也就是说矩阵B的列向量组可以由AX=0 的基础解系线性表示,所以R(B) <= n-R(A),故R(A)+R(B)小于等于n。
-
考研数学真题ln(1-x)的泰勒展开式是什么呀?
教师回复: 这里应该套用的是ln1+x的公式,因为x趋于0的,然后可以把-x带入
-
考研英语句子“What a difference a day makes!”能否译为“一天的变化真大
教师回复: 这是个感叹句,使用了倒装,顺过来说是 a day makes a difference. 某一天产生了重要的作用/ 某一天发生了一个变化。 用感叹语气,则是 某一天产生了多么大变化啊!(某一天和平时非常不一样);翻译则调整表达为: 多么与众不同的一天啊! 多么特别的一天啊!
-
为什么x趋于0时,为什么ln(cosx)等于-1/2 x^2?
教师回复: x趋于0,cosx的极限是1,所以ln(cosx)=ln(1-1+cosx),等价无穷小为-1+cosx,也就是等价无穷小为-1/2 x^2
- 金融类
- ACCA
- 证券从业
- 银行从业
- 期货从业
- 税务师
- 资产评估师
- 基金从业
- 国内证书
- CPA
- 会计从业
- 初级会计职称
- 中级会计职称
- 中级经济师
- 初级经济师
- 其它
- 考研




